Emotion Aware Music Generation

Introduction

In the last decade, there have been rapid advancements in deep-learning-based generative models such as generative adversarial networks (GANs) and variational autoencoders (VAEs). Models performing style transfer, image generation, super-resolution, and other impressive feats soon followed, showcasing the power of these types of models. Music generation has proven to be particularly interesting, as initial generative models struggled with more sequential data such as audio [1]. In the past few years, researchers have extended these models to musical domains to generate songs in specific genres [2]–[4].

Data Collection

We chose the EMOPIA dataset for this project [5]. The dataset contains 1078 clips from 387 songs in the piano-pop genre. These clips are sourced from YouTube and encoded in the MIDI format. The MIDI format is an intentional choice here since this standard encodes important musical features including specific instrument notes, tempo, and key with labels describing the arousal and emotional valence for various parts of the sequence. Each clip was annotated by one of four human annotators, where each label represents the quadrant in valence-arousal space corresponding to the emotions elicited by the song clip. The numbers of clips per quadrant are approximately evenly distributed, with 250, 265, 253, and 310 clips for quadrants 1, 2, 3, and 4 respectively. The EMOPIA dataset is particularly pristine, containing recordings of single-instrument (piano), emotionally-consistent clips. This streamlines audio analysis and reduces variation in timbre, dynamics, and other compositional characteristics.

Problem Definition

In recent years, there has been tremendous growth in video content available online, by way of movies, tv shows, and content creators. Instagram alone has 500k professional content creators, with an additional 30 million amateurs [6]. A majority of these videos use some kind of music in the background to convey emotions to the viewer. As more content is generated, there is naturally a greater demand for appropriate music, searching for which is a tedious task and opens the way to copyright issues.

We can make this task easier by using generative models to generate music that conveys a certain emotion. Depending on the creator’s intent, they can choose between different emotions and generate completely novel music scores for their content. Using AI-generated music, they save precious time and don’t have to worry about copyright issues.

Supervised Models

Methods

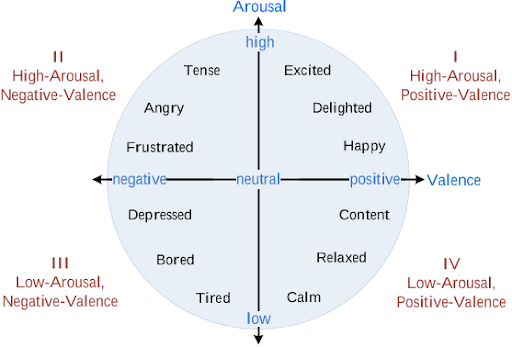
Our first task was to build supervised models to classify the emotion of each song clip. This is a multinomial classification problem in which the model must classify each song clip into one of the quadrants in valence-arousal space given by the Russell circumplex model (see Appendix) [7]. We experimented with a variety of supervised models, namely Decision Trees, Random Forests, Logistic Regression, and k-Nearest Neighbors, as well as two, deep learning approaches to perform multinomial classification. For the latter two models, we selected a long short-term memory (LSTM) and a ShortChunkCNN_Res architecture. The LSTM architecture was selected because of LSTMs’ proficiency in classifying sequential data, of which music is a quintessential example [8]. The ShortChunkRNN was selected as it was referenced in the EMOPIA dataset paper.

Two methods were employed to train and evaluate the classical models. In the first, an 80/10/10 train-validation-test split was constructed, resulting in 876 training samples, 114 validation samples, and 88 testing samples from the EMOPIA dataset. In the second approach, we employ k-fold cross-validation (k=10), allowing us to use all the data in training for the supervised models. For simplicity, the deep learning models were trained on the train/validate/test split rather than k-fold cross-validation.

Given a MIDI file, there is an abundance of feature representations from which to choose. We experimented with several signal analysis techniques including pitch density distributions, “piano roll” time-frequency matrices, and note transition matrices to feed into our models. Ultimately, we found the piano roll representation to perform best. A piano roll is a time-frequency matrix where each row represents a different MIDI pitch (i.e., note) and each column represents a time slice of 1/100 seconds.

We then performed backward feature selection using Recursive Feature Elimination with Cross-Validation (RFECV). Since RFECV is model-dependent (i.e. it uses each model to provide feature importances), this reduced our dimensionality from 128 features to 22, 87, and 25 features for DT, RF, and Logistic Regression respectively.

Results

Table 1: Supervised Model Performance Metrics

Model	10-fold CV Accuracy	CV Std. Dev.	Weighted Avg. F1
Decision Tree	.523	.031	.509
Random Forest (1)	.552	.053	.537
Logistic Regression	.439	.067	.397
k-NN (2)	.364	.149	.398

(1) Optimal random forest consisted of 150 estimators.

(2) Optimal k-NN classifier consisted of 28 neighbors.

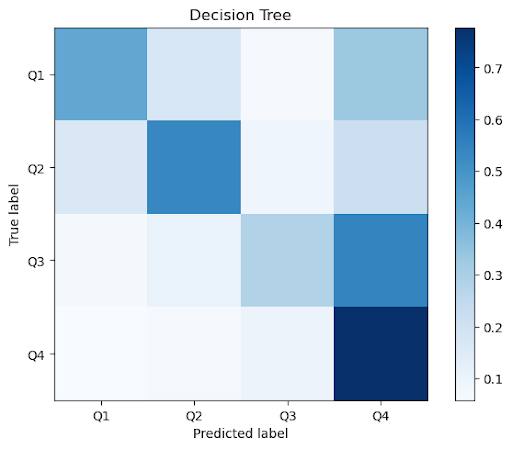
Figure 1: Optimal Decision Tree

Table 2: Sequential Model Performance Metrics

Model	Train Acc.	Test Acc.
LSTM (Vanilla)	.8953	.5227
ShortChunkCNN_Res	.999	.455

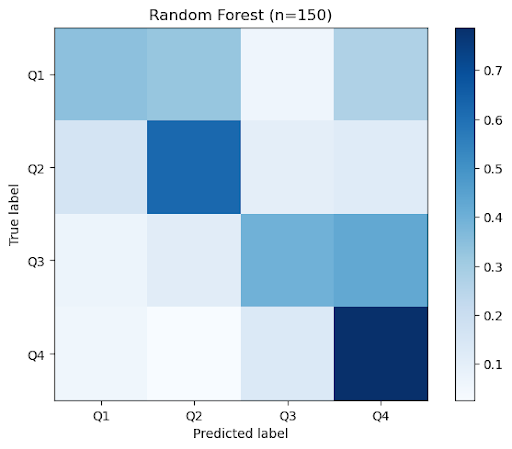
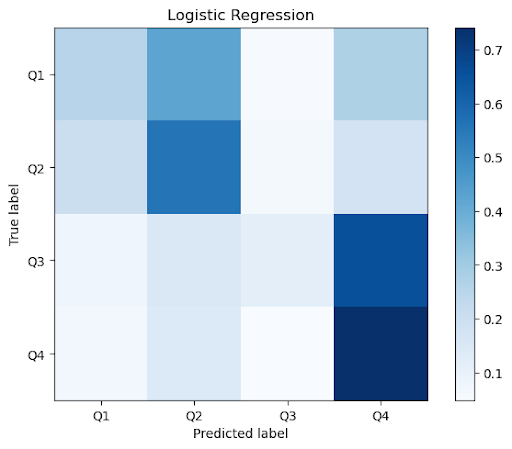
Figure 2a: Aggregate confusion matrices across k=10 folds for classical methods

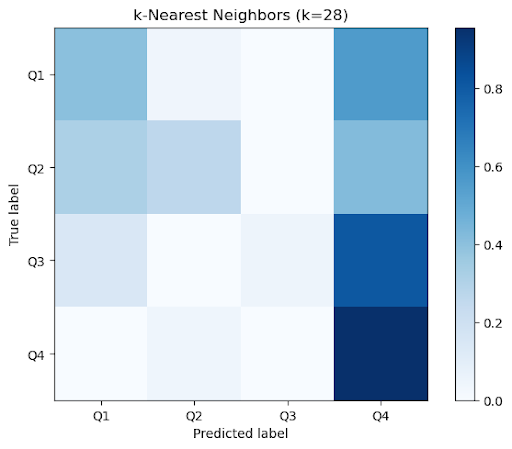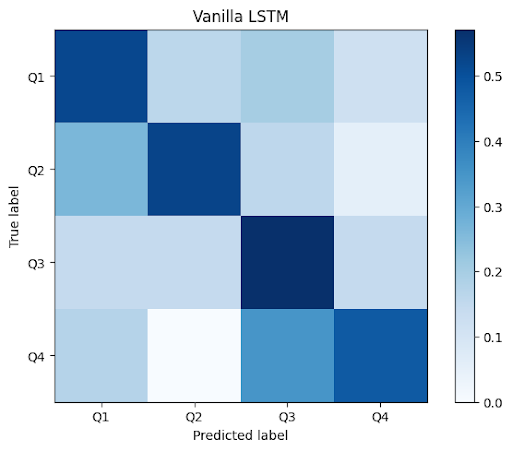
Figure 2b: Confusion matrix for Vanilla LSTM on Test Set

Figure 2b

Unsupervised Models

Methods

In order to generate music, we looked at various generative models which have an encoder-decoder architecture that can be leveraged to learn a latent representation of the data and generate songs using that latent representation. We first experimented with VAEs and found that the latent representation learned by VAEs didn’t have a defined structure or separation between the different emotion classes which made it hard to generate music for a specific emotion. We further looked into another type of generative models, namely GANs. GANs consist of a generator and critic which are pitted against each other in a zero-sum game. The goal of the generator is to create samples that the discriminator can’t distinguish from the real examples and the goal of the discriminator is to identify between the real and fake examples generated by the generator.

Figure 3a: General Architecture of GANs

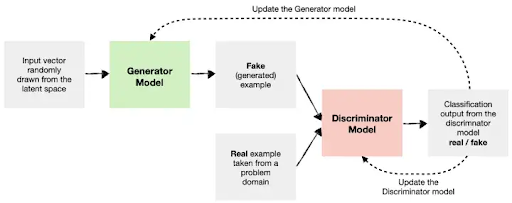
Figure 3a

Figure 3b: Modified GANs with label information incorporated

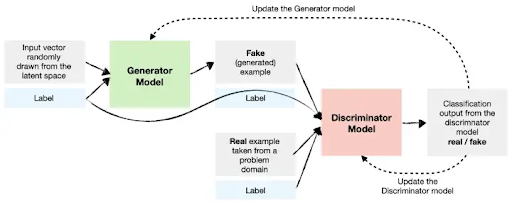
Figure 3b

After surveying the existing literature around music generation, we found the MuseGAN [9] model, which was built to generate multi-track songs and closely aligned with our task. We modified its architecture to accept single track songs and emotion information and trained it on the EMOPIA dataset.

Figure 4: MuseGAN model architecture

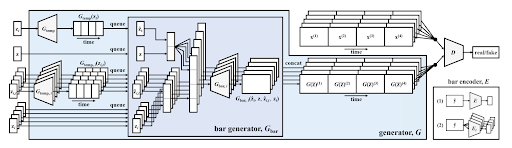
Data Preprocessing for GAN

To generate a dataset for this model, we sampled 4842 samples of 64 timesteps (~40s) from the original EMOPIA dataset’s 1078 annotated clips. One such sample is shown in Figure 5.

Figure 5: Sampled sequence for GAN training

We generated two different processed datasets, one with and one without the emotion information from the EMOPIA dataset in order to compare the stability of training and fidelity of generated songs in both cases. This also acts as an ablation and helps us learn the value added by incorporating the emotion information into the model.

Training the Model

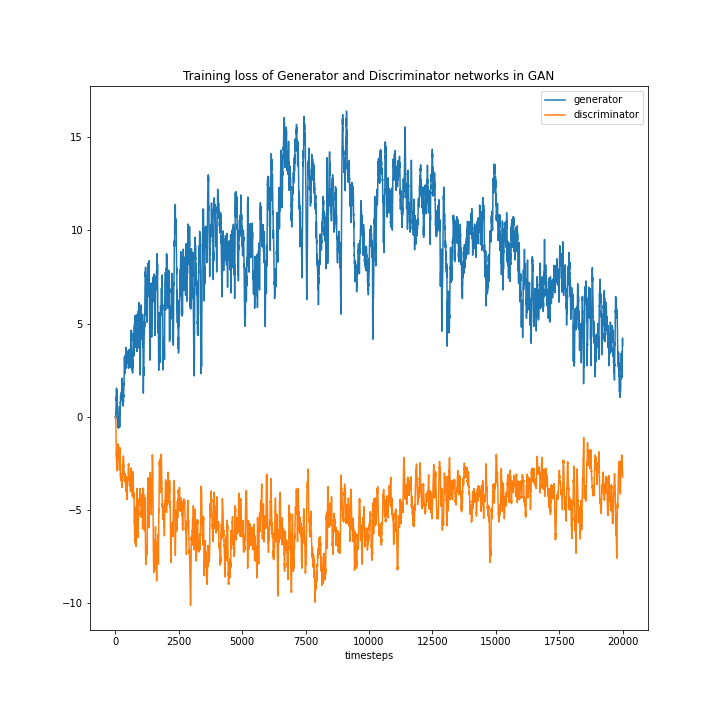
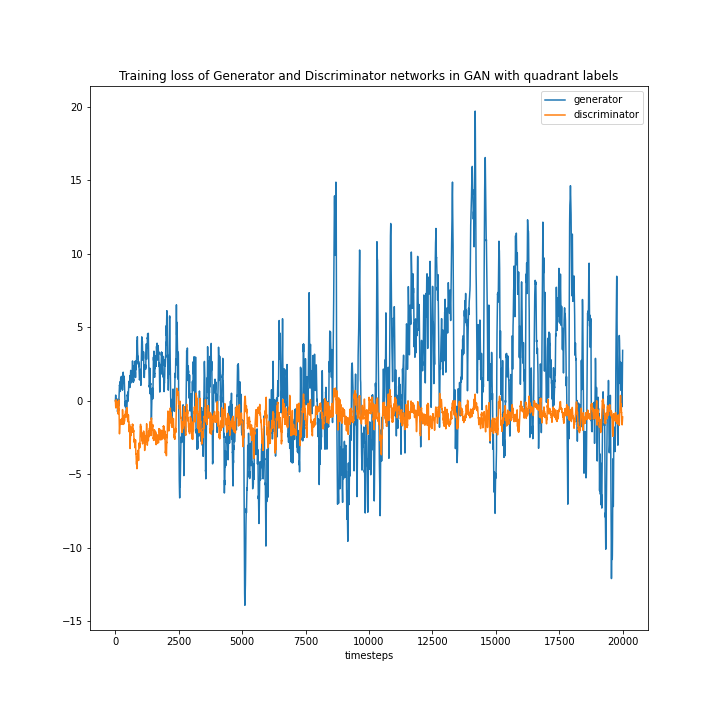
The model was trained for 20k steps, with each step training on a batch of 16 samples. The training loss for both with and without label augmentation is shown in Figure 6.

Figure 6: Loss plots of generator and discriminator without label augmentation (left) and with label augmentation (right)

Without label augmentation (left), we noticed that the training loss for the generator is quite high compared to the discriminator and while in the later timesteps, it shows a converging trend, it still is not quite there. The loss also has a high variability, which is commonly observed in GANs. Incorporating the label information makes the losses converge (right). While there is still a lot of variability in the loss function, the average loss values of the discriminator and the generator are about the same. The results are much better compared to training without the label augmentation.

We also experimented with different learning rates for the generator and discriminator as well as incorporating learning rate decay. From our experiments we found that the most stable model is achieved when the learning rate of the generator is slightly higher than the discriminator. This provides the generator ample opportunities to learn and keep up with the discriminator. We can see the same trend in the loss plots in Figure 6, where the discriminator is initially strong compared to the generator, but the generator catches up later on in the training session. In the 0 sum game format, having too strong a discriminator or the generator can result in diverging loss and the network not learning anything. So, it’s important to keep them in check and tune the hyperparameters accordingly.

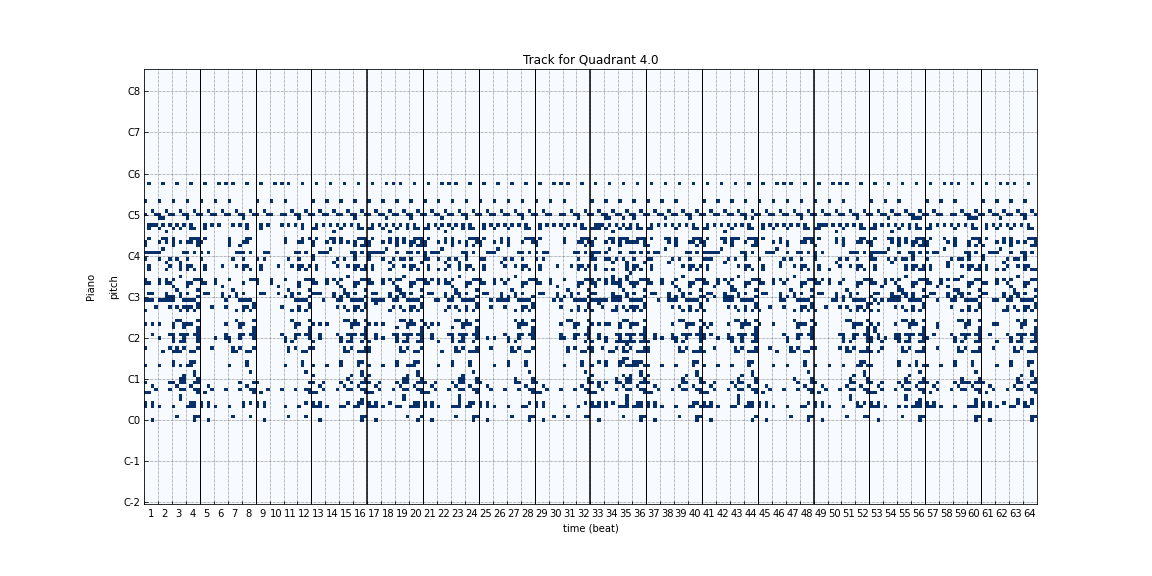
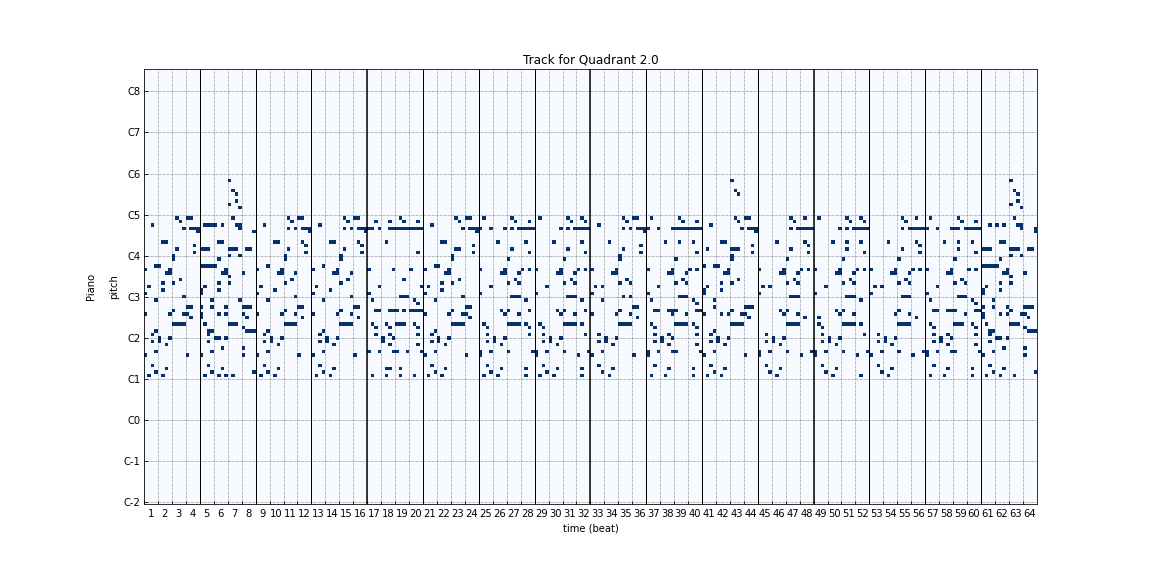
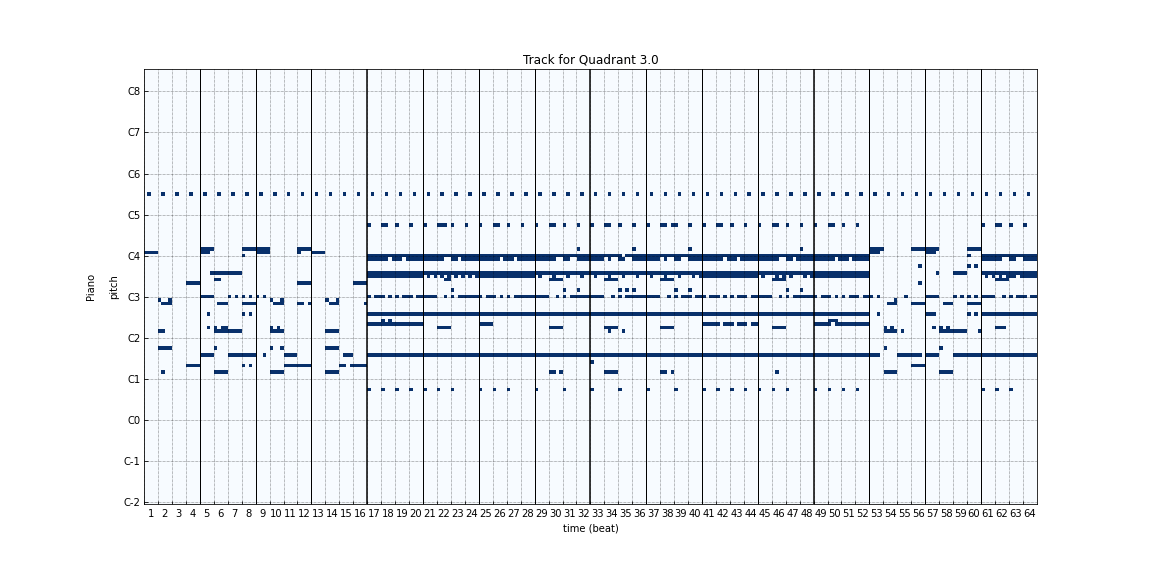
Figure 7: Generated tracks at different timesteps during the training process using a random seed/noise passed to the generator. (0, 100, 1k, 10k, 20k)

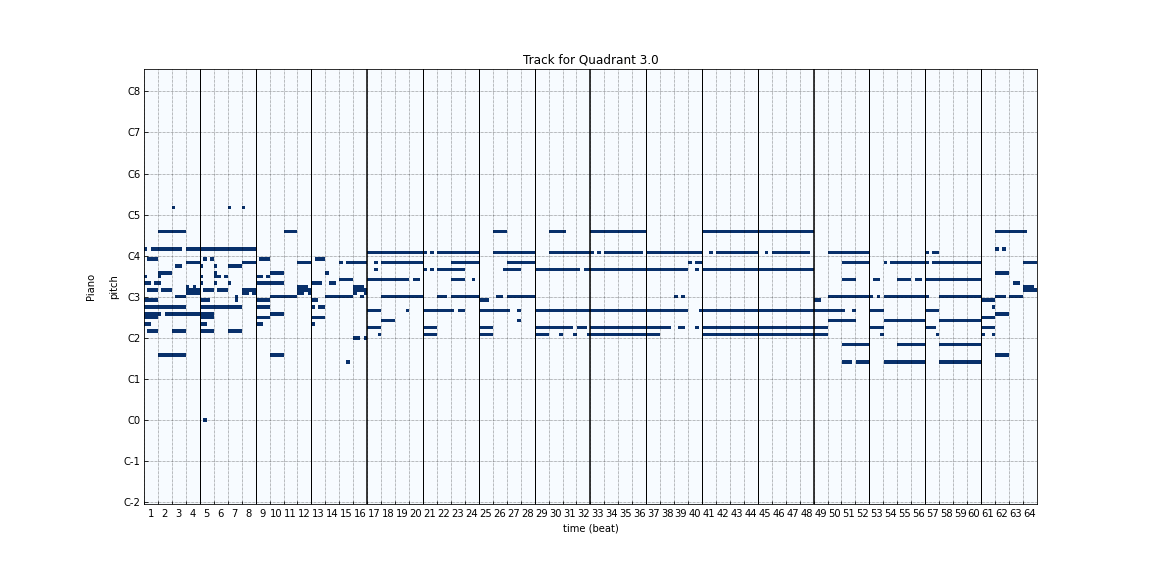In order to assess the qualitative performance of the generated songs during the training process, we sampled songs using a random latent passed to the generator at different timesteps during the training process. Looking at the generated music, we can see that as training progresses, there is more and more structure to the songs. The music generated initially has a lot of noise, and as training progresses the generated songs look more and more like a real piece of music.

Results

In order to generate songs after training, we pass a random latent representation augmented with emotion labels to the generator. Since, apart from the convergence of loss between the generator and discriminator, there aren’t many ways to assess the performance of the GAN model, we took many such random samples and assessed the quality of generated samples manually. Below are some of the samples generated by our model for different emotions:

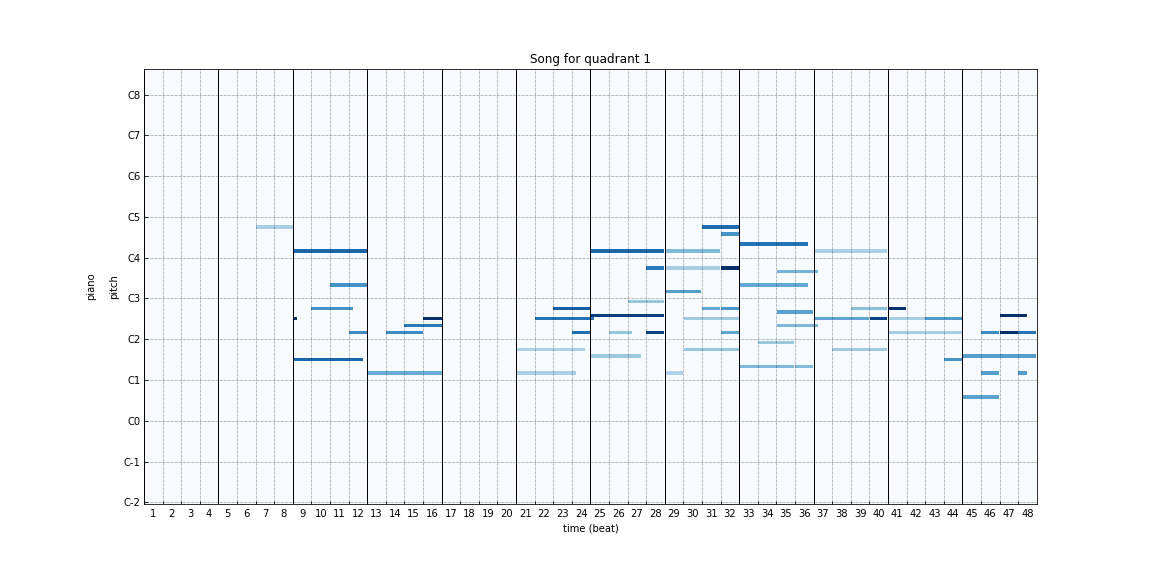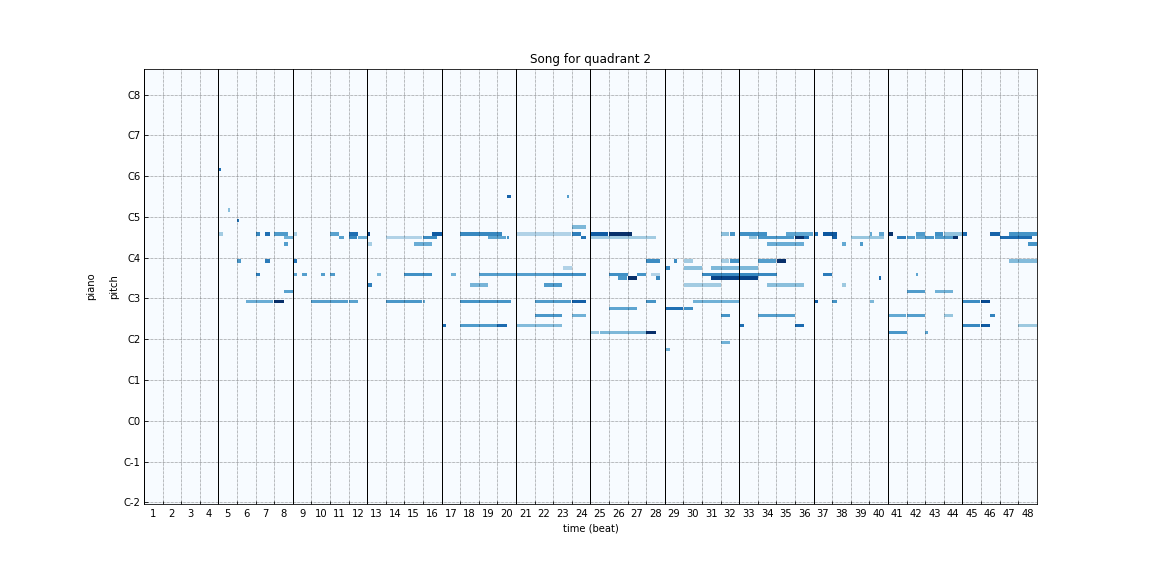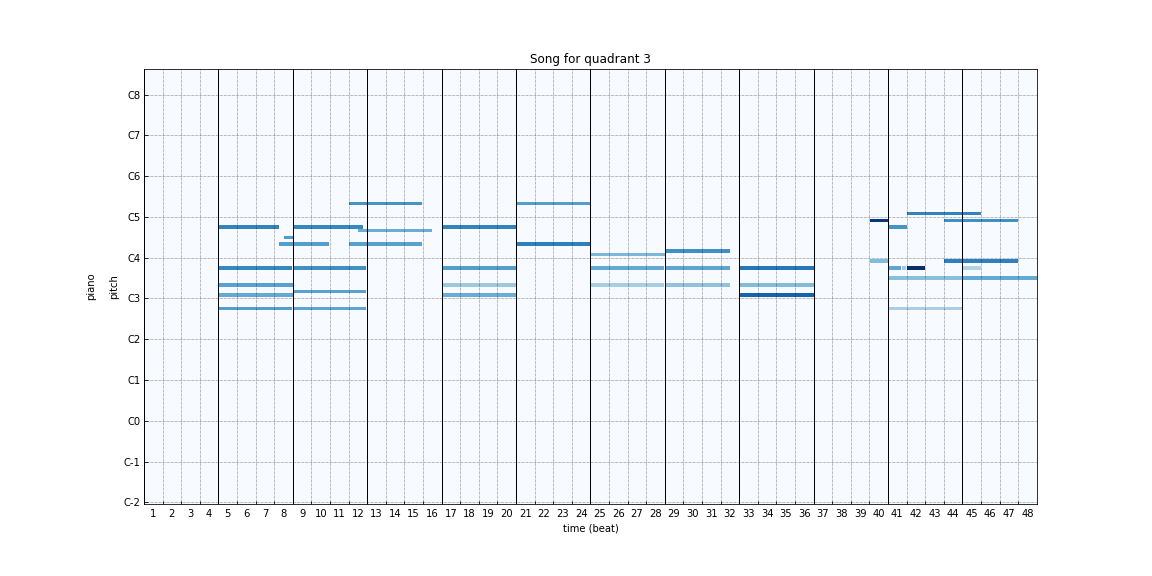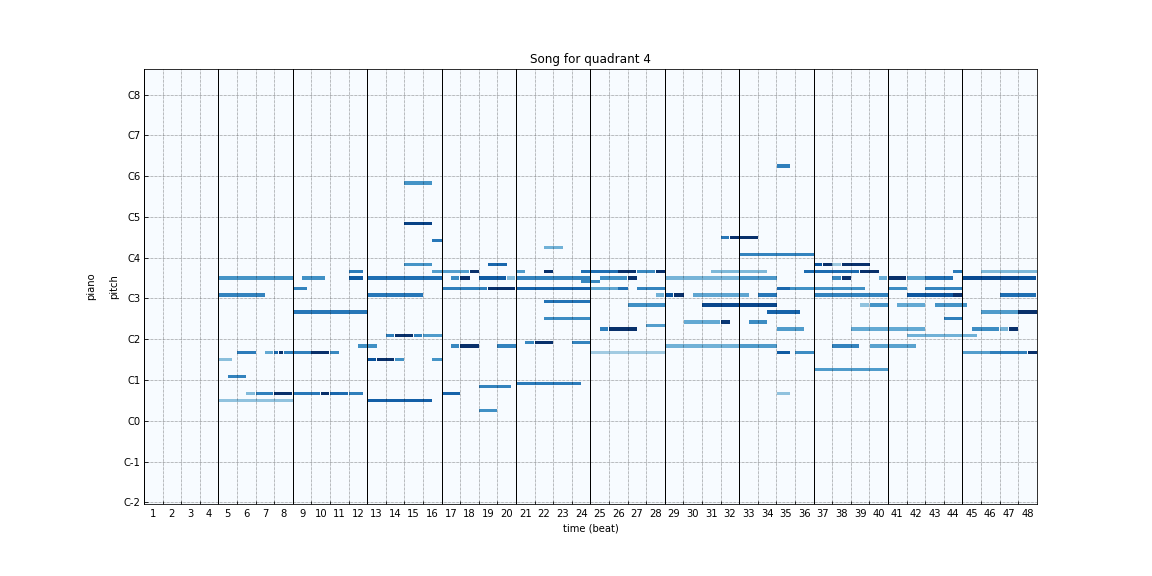The sounds generated are quite distinct and come close to conveying the emotions that were requested. Consistent with human characterizations of happy/exciting versus sad/somber songs, the songs with lower arousal values seem to have fewer notes or more notes in the lower registers whereas the ones with higher arousal seem to have more notes or more notes in the higher register.

Discussion

Our supervised models trained on the dataset achieve similar accuracy to what the authors have published in their paper. Simpler models like KNN and Logistic regression trained on the piano roll time-frequency matrix achieve an accuracy of 43-45% on the cross-validation data, whereas Decision Tree and Random Forest achieve 52.3% and 55.2% accuracy respectively. Our best model, the Random Forest model, achieves a weighted average F1 score - where F1 scores for each class are weighted by their proportion of the data and averaged - of 0.537 on the cross-validation data.

While the performance is much better than chance (i.e. 25% chance of guessing the right quadrant), it’s still not very impressive. Part of this could be due to the complexity of the data and the presence of a temporal component, which simpler models aren’t able to capture.

Looking at the confusion matrix, we find that most of the misclassifications by the tree-based models are from predicting the 4th quadrant in cases where the true label is in either the first or the third quadrant. Furthermore, we found the recall score to be the smallest for the third quadrant across all models. Since the data points in those quadrants share some similarities, we believe that most of the misclassified samples are near the boundary. Qualitatively, it appears that songs with positive valence and higher arousal are more easily classified. Thus, since third-quadrant songs are characterized by depressed, somber emotions (i.e., negative valence, low arousal), we find the models struggle most with examples of this category.

For the Deep Learning Approaches, the large gap in training accuracy and test accuracy indicates that overfitting has occurred. We attempted to rectify this using weight decay. Although this was helpful in improving generalization, there was still a large (but reduced) gap between test and train accuracy. Future work could further target overfitting by introducing data augmentation and by collecting more training data. We would also like to explore the ShortChunkCNN_Res model suggested by the Dataset authors. Work on this was started as part of this project, but could not be completed because of its complexity and time constraints.

The modified MuseGAN model trained on our dataset gives good performance with distinct generated music for each emotion. Currently the model generates short snippets of music (~40s) for a given label, which can be extended to generate longer music scores. Training the model for longer duration or on more training data might also give us even better performance which we will pursue in the future.

Conclusion

In summary, the supervised models saw reasonable success in the emotion classification of the raw MIDI clips task, achieving a test accuracy of 55.2% with a random forest model. The GAN model gives good performance and generates novel music for a given emotion with distinct signatures, which can directly be used for multiple use cases.

References

J.-P. Briot, G. Hadjeres, and F.-D. Pachet, “Deep Learning Techniques for Music Generation – A Survey.” arXiv, Aug. 07, 2019.
R. Guo, I. Simpson, T. Magnusson, C. Kiefer, and D. Herremans, “A variational autoencoder for music generation controlled by tonal tension.” arXiv, Oct. 14, 2020. doi: 10.48550/arXiv.2010.06230.
J. Grekow and T. Dimitrova-Grekow, “Monophonic Music Generation With a Given Emotion Using Conditional Variational Autoencoder,” IEEE Access, vol. 9, pp. 129088–129101, 2021, doi: 10.1109/ACCESS.2021.3113829.
J. Engel, K. K. Agrawal, S. Chen, I. Gulrajani, C. Donahue, and A. Roberts, “GANSynth: Adversarial Neural Audio Synthesis,” presented at the International Conference on Learning Representations, Sep. 2018.
H.-T. Hung, J. Ching, S. Doh, N. Kim, J. Nam, and Y.-H. Yang, “EMOPIA: A Multi-Modal Pop Piano Dataset For Emotion Recognition and Emotion-based Music Generation.” arXiv, Aug. 03, 2021. doi: 10.48550/arXiv.2108.01374.
“Number of online content creators worldwide by platform 2020,” Statista.
J. A. Russell, “A circumplex model of affect,” J. Pers. Soc. Psychol., vol. 39, pp. 1161–1178, 1980, doi: 10.1037/h0077714.
L.-C. Yang, S.-Y. Chou, and Y.-H. Yang, “MidiNet: A Convolutional Generative Adversarial Network for Symbolic-domain Music Generation.” arXiv, Jul. 18, 2017. doi: 10.48550/arXiv.1703.10847.
H.-W. Dong, W.-Y. Hsiao, L.-C. Yang, and Y.-H. Yang, “MuseGAN: Multi-track Sequential Generative Adversarial Networks for Symbolic Music Generation and Accompaniment.” arXiv, Nov. 24, 2017. doi: 10.48550/arXiv.1709.06298.